空间精度量测技术是一种在机床上有效得知机器精度的技术之一,本文将简述此技术的益处,和透过此技术能分析整机空间中任一点之误差,并且对机台精度做预估,预先分析精度检验路径精度,最终能对机台做补偿,以提升机台精度表现,现今此技术仍具有一定门坎,希望借由本文能让读者进一步了解此技术。
线性轴几何误差与机构链的关联
机床所有误差来源中静态误差占了70%而几何误差为静态误差中的主要成分,其可分为部件误差以及位置误差,部件误差系指误差随部件移动位置不同而有不同的误差值,可视为一误差函数对应不同位置,例如:定位精度、真直度、PITCH、ROLL、YAW。位置误差则不随移动而改变,是一固定数值,例如:垂直度、旋转中心误差……等。
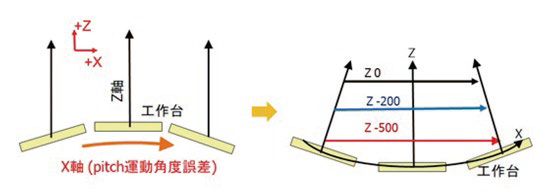
图1 运动角度误差与不同位置定位精度之关系
五轴机床一般含有三个线性轴以及两个旋转轴(包含一旋转轴、一倾斜轴),在线性轴部分,由三个线性轴所组成的坐标系统中,含有三个因垂直度造成的位置误差,以及每一线性轴中共含有6个自由度部件误差,故在三个线性轴所组成的坐标系统中,共含有二十一项误差,而一旋转轴中共有5个位置误差以及6个自由度部件(定位精度、两方向真直度、PITCH、ROLL、YAW)误差共11项误差,因此五轴机床一共含有线性轴21项误差加上两个旋转轴22项误差,共有43个误差项。
空间精度误差来源中,除原有的零部件质量及加工组装技术所造成的定位精度与真直度外,运动角度是一大关键(PITCH、ROLL、YAW),由图1可知,当X轴运动过程中产生角度误差时,会使得定位精度在不同Z位置造成影响,此影响因子也会同时表现在真直度误差里。空间精度误差补偿功能
前述的运动角度关系在会被不同线性轴堆栈的关系所影响,因此必须针对机台构型建立机构链,以掌握刀尖与工件的相对位置,使得线性轴与旋转轴的堆栈关系能完整建立在控制器内,使其运算及补偿机制能够正常运作。其简单概念是由刀端点出发经过各驱动轴后至工件坐标原点而形成一个封闭架构。
故如能将各线性轴之6自由度误差量测出来,再按照其构型建立相对应之误差模型,即可计算出空间各位置之刀尖点误差,如图2所示。
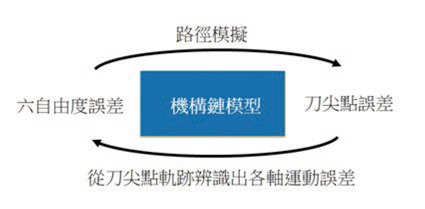
图2 机构链模型流程图
目前机床业界常用之CNC三大商用控制器,皆可支持空间精度补偿,并可按照空间精度补偿方式分为欧系(HEIDENHAIN、SIEMENS)与日系(FANUC)两种补偿方式。欧系控制器系利用机构链补偿、日系控制器则是利用空间格点方式补偿。
举例来说,假设一机床X、Y、Z三轴各轴量测各10点6自由度部件误差,则在欧系控制器上则仅需输入X、Y、Z三轴各10点之6自由度部件误差信息,控制器即能借由此误差讯息,透过机构链对空间中各位置做计算补偿。如图3所示,补偿点数如需增加,则需增加量测点数,然而日系控制器则需要计算出空间中每一点、即10×10×10共1000点位置之误差值,并按照控制器之排列规则输入。故为了要计算出上述空间中各点之误差值,必须建立其机构链模型(kinematicmodel),借由输入各轴六自由度误差,并且按照不同机型之机构链模型,得以计算出空间任一位置之刀尖点误差值。另一方法则可利用激光追踪仪(eTalonLaserTracer)即可量测到空间中各点之误差,但该量测仪器成本稍高且量测时间较长,本文此次暂不讨论此方法。
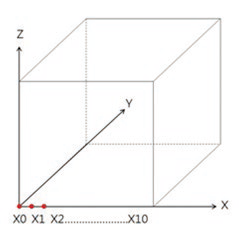
图3 空间中各误差点
将上述技术与实际机台补偿结合时,还需要将量测位置与实际补偿之刀长信息一同做输入进误差模型里,因为需要将实际量测位置回推至机台原点(主轴鼻端)。空间精度误差分析技术
有鉴于此,本中心所开发之空间精度分析技术,可将各轴六自由度误差,借由不同机构链之误差模型,分析出改机器空间各点之刀尖点误差,并可模拟不同误差(真直度、角度、垂直度)将空间误差可视化,如图4所示,能输入量测信息、机台机构链、量测镜组与主轴鼻端OFFSET等信息,并可将针对各平面误差,输入不同刀长、垂直度误差、坐标位置以分析各平面之误差,在额外的功能方面,分析功能可将三轴共21项误差进行分析,将整机空间精度误差可视化,让使用者能更清楚了解到机台整机空间精度。
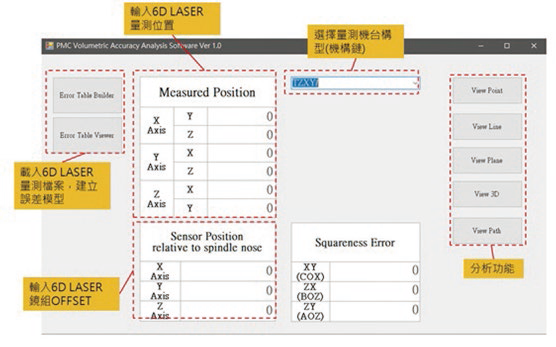
图4 误差模型建立功能开发分析软件以提升机台精度表现
透过市售6D激光量测仪器,能快速得知机台线性轴各自由度误差,本中心所开发之空间精度量测分析软件能直接汇入量测档案,未来将可结合业界现
有常见仪器,激光干涉仪、自动视准仪、水平仪等量测设备,并不一定受限于量测仪器之限制,仪器使用自由度及方便性提高。
按照各机型之机构链做误差分析将有助于误差可视化,可帮助使用者快速了解机器误差,并且能快速调整各误差项做分析模拟,以预估不同组装精度所造成机台精度的变化,还能做检验路径精度预估或加工路径精度预估,最终能透过补偿功能产生相对应之补偿数据结合控制器补偿机制,以改善整机机台空间精度误差,以提升机台现有精度表现。
 金属板材成形之家-MFC金属板材成形杂志/金属成形商务咨询(北京)有限公司-MFC《金属成形智造》杂志
金属板材成形之家-MFC金属板材成形杂志/金属成形商务咨询(北京)有限公司-MFC《金属成形智造》杂志